点击下载 .ipynb 代码

目标: 现在有一个字符串 INPUT = "Ark", 需要对其进行 MD5 算法加密.¶

Jupyter Notebook 是具体讲解 MD5 底层原理, 结合 RFC-1321 文档分析的.

RFC-1321-URL: https://www.rfc-editor.org/rfc/pdfrfc/rfc1321.txt.pdf

篇幅会比较长, 适合一步一步入门学习, 但实际意义上的实现, 需要考虑性能问题, 按照 .py 程序的来.

MD5 算法加密的过程分为三步:

  • 处理原文
  • 设置初始值
  • 加密运算
In [ ]:
'''
# System --> Windows & Python3.8.0
# File ----> jupyter.ipynb
# Author --> Illusionna
# Create --> 2024/04/27 23:01:42
'''
# -*- Encoding: UTF-8 -*-


import os
import platform

def cls() -> None:
    os.system('')
    try:
        os.system(
            {'Windows': 'cls', 'Linux': 'clear'}[platform.system()]
        )
    except:
        print('\033[H\033[J', end='')
cls()

"Ark" 可以看作 3 个 utf-8 编码的字符共同构成的.

"Ark" = "A" + "r" + "k"

把 "A" 转化成 utf-8 编码下的 0-1 比特流: $$ {\rm ``A"} \longmapsto 65(Decimal) \longmapsto 41(Hexadecimal) \longmapsto 01000001(Binary) $$

同样的, 得到 "Ark" 在 utf-8 编码下的 0-1 比特流: $$ {\rm ``Ark"} \longmapsto 01000001,\ 01110010,\ 01101011(Binary) $$

In [ ]:
class TRANSFORM:
    """
    转化类.
    """

    INPUT = 'Ark'

    @staticmethod
    def TransformHexadecimal(input:str, mode:str='utf-8') -> str:
        """
        字符串转化十六进制字符串.

        例如: input = "A" 且 utf-8 编码
            则 \x41 是十进制 65 对应的十六进制 41, 也是 ASCII 码的 "A"
        """
        return ''.join([rf'\x{byte:02x}' for byte in input.encode(mode)])

    @staticmethod
    def TransformBinary(input:str, mode:str='utf-8') -> str:
        """
        字符串转化二进制 0-1 字符串.

        例如 input = "A" 且 utf-8 编码
            则 01000001 对应 ASCII 码的 "A", 也是 utf-8 下的 "A"
        """
        return ''.join(format(byte, '08b') for byte in input.encode(mode))

    @staticmethod
    def ViewHexadecimal(input:str, mode:str='utf-8') -> str:
        """
        查看十六进制字符串, 方便观察, 但不能运算.
        """
        return ' '.join([rf'\x{byte:02x}' for byte in input.encode(mode)])

    @staticmethod
    def ViewBinary(input:str, mode:str='utf-8') -> str:
        """
        查看二进制字符串, 方便观察, 但不能运算.
        """
        return ' '.join(format(byte, '08b') for byte in input.encode(mode))


print(f'"\033[32m{TRANSFORM.INPUT}\033[0m" \033[31m|---->\033[0m \033[33m{TRANSFORM.ViewBinary(input=TRANSFORM.INPUT, mode="utf-8")}\033[0m')

"Ark" |----> 01000001 01110010 01101011
第一步: 处理原文¶

MD5 算法把信息 (0-1 比特流) 以 512 比特位为一组分组处理, 因此需要进行填充算法.

"Ark" 的比特流 $01000001,\ 01110010,\ 01101011(Binary)$, 长度是 $3\times8=24$, 而 $512\div8=64$ 字节.

也就是说, 现在只有 3 字节是有效信息, 还有 $64-3=61$ 字节无内容.

MD5 填充算法规定:

有效信息流的下一字节首位是 1 比特, 其余所有位全为 0 比特, 并且最后 8 字节存放有效信息比特流长度. $$ 01000001,\ 01110010,\ 01101011,\mid \underbrace{10000000,\ 00000000,\cdots,\ 00000000}_{53 字节},\mid \underbrace{00011000,\ 00000000,\cdots,\ 00000000}_{8字节} $$

最后 8 字节的第一字节 $00011000$ 对应十进制就是 24, 也就是有效信息的比特流长度.

简言之, 在原文基础上填充一个 "$10000000$" 比特流, 然后新构成的比特流长度与 512 取余, 如果结果不为 448, 则就需要再填充一系列的 "$00000000$", 使得整体与 512 取余结果为 448, 并且最后额外追加 8 字节存储原文比特流长度. $$ (3\times8+1\times8+52\times8)\mod512=448 $$

设有效信息流字节长度为 $n$ (已知), 填充 0 字节流长度为 $m$ (未知). $$ \begin{align} (n\times8+1\times8+m\times8)\mod512&=448 \notag \\ &\Downarrow \notag \\ (n+1+m)\mod64&=56 \notag \\ &\Downarrow \notag \\ (n+1+m)&=56+64k,\ \ \ k=0,1,2,\ldots \notag \\ &\Downarrow \notag \\ 则通式:\ m&=64k+55-n,\ \ \ k=0,1,2,\ldots \notag \\ \end{align} $$

In [ ]:
class PADDING:
    """
    填充类.
    """

    def __init__(self, binary:str) -> None:
        self.__binary = binary
        self.__effectiveMessageLength = len(binary)

    def ZeroBitsPadding(self) -> str:
        """
        零比特填充.
        """
        self.__binary = self.__binary + '10000000'
        while ((len(self.__binary) % 512) != 448):
            self.__binary = self.__binary + '00000000'
        return self.__binary

    def DepositPadding(self) -> str:
        """
        有效信息存储填充.
        """
        string = bin(self.__effectiveMessageLength)[2:].zfill(64)
        return self.__binary + ''.join([string[i:i+8] for i in range(0, 64, 8)].__reversed__())


tmp: str = TRANSFORM.TransformBinary(input=TRANSFORM.INPUT, mode='utf-8')
obj = PADDING(binary=tmp)
tmpA = obj.ZeroBitsPadding()
print(tmpA)
print(f'\033[33m零比特填充后比特流长度: {len(tmpA)}\033[0m')
tmpB = obj.DepositPadding()
print(tmpB)
print(f'\033[33m有效信息存储填充后比特流长度: {len(tmpB)}\033[0m')

0100000101110010011010111000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
零比特填充后比特流长度: 448
01000001011100100110101110000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001100000000000000000000000000000000000000000000000000000000000
有效信息存储填充后比特流长度: 512
第二步: 设置初始值 (幻数)¶

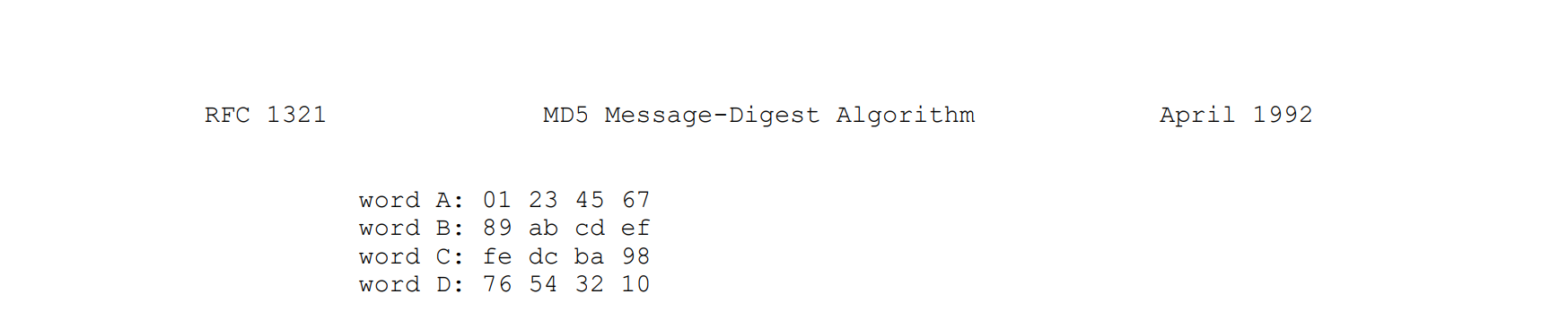
RFC-1321 规定标准 MD5 初始迭代的四个幻数 (每个幻数 32 比特位) 分别为:

  • word A = 0x67452301
  • word B = 0xefcdab89
  • word C = 0x98badcfe
  • word D = 0x10325476

注意计算机比特位是从右往左 (小端位), 每八个位一个字节, 所以用十六进制表示会和 RFC 文档的幻数掉序.

No description has been provided for this image
In [ ]:
class MAGIC:
    """
    初始化幻数类.
    """

    A = 0x67452301
    B = 0xefcdab89
    C = 0x98badcfe
    D = 0x10325476

    @staticmethod
    def ViewBinary() -> None:
        """
        查看幻数的比特流.
        """
        def Function(hexadecimalNumber:int) -> None:
            decimalNumber = int(hexadecimalNumber)
            hexadecimalBinary = ' '.join([format(decimalNumber, '032b')[i:i+8] for i in range(0, 32, 8)])
            decimalBinary = ' '.join([str(int(binary, 2)) for binary in hexadecimalBinary.split()])
            return (hexadecimalBinary, decimalBinary)

        print(f'word A --> 十六进制: {hex(MAGIC.A)} 十进制: {MAGIC.A}\n\t二进制比特流: {Function(MAGIC.A)[0]}\n\t十进制数字流: {Function(MAGIC.A)[1]}')
        print(f'word B --> 十六进制: {hex(MAGIC.B)} 十进制: {MAGIC.B}\n\t二进制比特流: {Function(MAGIC.B)[0]}\n\t十进制数字流: {Function(MAGIC.B)[1]}')
        print(f'word C --> 十六进制: {hex(MAGIC.C)} 十进制: {MAGIC.C}\n\t二进制比特流: {Function(MAGIC.C)[0]}\n\t十进制数字流: {Function(MAGIC.C)[1]}')
        print(f'word D --> 十六进制: {hex(MAGIC.D)} 十进制: {MAGIC.D}\n\t二进制比特流: {Function(MAGIC.D)[0]}\n\t十进制数字流: {Function(MAGIC.D)[1]}')


MAGIC.ViewBinary()

word A --> 十六进制: 0x67452301 十进制: 1732584193
	二进制比特流: 01100111 01000101 00100011 00000001
	十进制数字流: 103 69 35 1
word B --> 十六进制: 0xefcdab89 十进制: 4023233417
	二进制比特流: 11101111 11001101 10101011 10001001
	十进制数字流: 239 205 171 137
word C --> 十六进制: 0x98badcfe 十进制: 2562383102
	二进制比特流: 10011000 10111010 11011100 11111110
	十进制数字流: 152 186 220 254
word D --> 十六进制: 0x10325476 十进制: 271733878
	二进制比特流: 00010000 00110010 01010100 01110110
	十进制数字流: 16 50 84 118
第三步: 加密运算 (更确切地说, MD5 并不是加密算法), 分为位运算和迭代¶

<1> 位运算

四个非线性的辅助函数: $$ \begin{align} F(X,Y,Z) &= (X\&Y) \mid ((\sim X)\&Z) \notag \\ G(X,Y,Z) &= (X\&Z) \mid (Y\&(\sim Z)) \notag \\ H(X,Y,Z) &= X\wedge Y\wedge Z \notag \\ I(X,Y,Z) &= Y\wedge (X\mid (\sim Z)) \notag \\ \end{align} $$

No description has been provided for this image

除此之外还有一个特殊的辅助函数, 循环左移: $$ {\rm LoopShiftLeft}=\mathscr{L}(X,s)= (X<<s)\mid(X>>(32-s)) $$

No description has been provided for this image

$X[k]$ 是一个连续的 32 位比特构成的整数.

按照作者在 RFC-1321 中规定, $s$ 的标准取值随迭代次数是固定的. $$ [7,12,17,22,7,12,17,22,7,12,17,22,7,12,17,22,5,9,14,20,\ldots\ldots,6,10,15,21]_{1\times64} $$

No description has been provided for this image

图中的 $T_i$ 是固定的 64 个整型常量, 计算公式: $$ T_i = \lfloor \mid \sin(i+1) \mid\times4294967296 \rfloor,\ \ \ i=1,2,\ldots,64\ 是弧度制 $$

$$ 4294967296(Decimal)=10000000,00000000,00000000,00000000(Binary) $$

No description has been provided for this image
In [ ]:
import math


class AUXILIARY:
    """
    辅助函数类.
    """

    F = lambda X,Y,Z:   (X & Y) | ((~X) & Z)
    G = lambda X,Y,Z:   (X & Z) | (Y & (~Z))
    H = lambda X,Y,Z:   X ^ Y ^ Z
    I = lambda X,Y,Z:   Y ^ (X | (~Z))
    L = lambda X,s:     (X << s) | (X >> (32 - s))
    T = lambda i:       int(abs(math.sin(i)) * (1 << 32))


print(f'12 弧度 --> T(12) 的十进制\033[33m {AUXILIARY.T(12)}\033[0m --> 十六进制\033[33m {hex(AUXILIARY.T(12))}\033[0m')
print(f'十进制 1 循环左移 7 位:\033[33m {AUXILIARY.L(1, 7)}\033[0m')

12 弧度 --> T(12) 的十进制 2304563134 --> 十六进制 0x895cd7be
十进制 1 循环左移 7 位: 128

<1> 迭代

In [ ]:
s = 4 * [7, 12, 17, 22] + 4 * [5, 9, 14, 20] + 4 * [4, 11, 16, 23] + 4 * [6, 10, 15, 21]

print(f'有效信息: "{TRANSFORM.INPUT}"')
input = TRANSFORM.INPUT.encode('utf-8')     # 按照 utf-8 编码解析成字节流.
print(f'有效信息字节流长度: {len(input)}, 比特流长度 {len(input) * 8}')

有效信息: "Ark"
有效信息字节流长度: 3, 比特流长度 24
In [ ]:
# 按照字节为单位, 计算有效信息每字节对应的十进制数值, 并存入列表.
# ----------------------------------------------------
# 不会一次将所有元素都加载到内存中, 而是在需要时逐个处理, 因此可以节省内存空间, 但速度会降低.
decimalList = list(map(lambda x: x, input))
# ----------------------------------------------------
# 一次性将字节流中所有元素加载到内存, 再构建新的列表对象存储全部元素, 速度快, 但占用内存多.
decimalList = list(input)
# ----------------------------------------------------
# 根据需要, 选择合适的处理步骤, 示例是 "Ark" 3 字节 24 比特, 所以后者比较合适.
# ----------------------------------------------------
print('\033[33m有效信息字节流构成的十进制列表\033[0m')
decimalList

有效信息字节流构成的十进制列表
Out[ ]:
[65, 114, 107]
In [ ]:
bitsLength = len(decimalList) * 8
decimalList.append(int('10000000', 2))      # 把 "10000000" 比特流转化成十进制 128 添加到十进制列表.
print(f'\033[33m添加 "10000000" 比特后十进制列表: {decimalList}\033[0m')

添加 "10000000" 比特后十进制列表: [65, 114, 107, 128]
In [ ]:
# 零比特填充.
while ((len(decimalList) * 8 + 64) % 512) != 0:
    decimalList.append(int('00000000', 2))  # 把 "00000000" 比特流转化成十进制 0 添加到十进制列表.
print(decimalList)
print(f'\033[33m零比特填充后比特流长度: {len(decimalList) * 8}\033[0m')

[65, 114, 107, 128, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
零比特填充后比特流长度: 448
In [ ]:
# 有效信息存储填充, 把有效信息 "Ark" 的比特流长度 (十进制 24) 存储到十进制列表尾部八字节.
for idx in range(0, 8, 1):
    decimalList.append((bitsLength >> (8 * idx)) & 0xff)      # 这里强制与 "11111111" 进行 & 运算.
print(f'\033[33m有效信息存储的十进制列表: {decimalList[-8:]}\033[0m')
print(f'\033[33m完整填充后字节流十进制列表: {decimalList}\033[0m')
# 如果不强制截断, 则可能会出现以下这种不正确的情况.
# 假设有效信息比特流长度 960
demo = """
bitsLength = 960
L = []
for idx in range(0, 8, 1):
    L.append(bitsLength >> (8 * idx))
print(L)
"""
# 结果为 >>> [960, 3, 0, 0, 0, 0, 0, 0]
# 而十进制列表的每个元素都是 8 比特位, 最大值才 255, 所以不可能出现 960 这个十进制数字.

有效信息存储的十进制列表: [24, 0, 0, 0, 0, 0, 0, 0]
完整填充后字节流十进制列表: [65, 114, 107, 128, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 24, 0, 0, 0, 0, 0, 0, 0]
In [ ]:
# 把十进制列表 decimalList 中顺序连续的 32 比特位逆置合成一个 32 位的整数值.
# 例如: [65, 114, 107, 128, ...] --> 65 114 107 128 --> 0x41 0x72 0x6B 0x80 --> 0x806B7241.
X = lambda a,b,c,d: (d << 24) | (c << 16) | (b << 8) | a
# 把 0x12345678 转化为 0x78563412, 即 32 位比特流高低位对换.
reverse = lambda x: (x << 24) & 0xff000000 | (x << 8) & 0x00ff0000 | (x >> 8) & 0x0000ff00 | (x >> 24) & 0x000000ff

# MD5 算法把信息 (0-1 比特流) 以 512 比特位为一组分组处理, 对每组迭代.
groups: int = len(decimalList) // 64
(A, B, C, D) = (MAGIC.A, MAGIC.B, MAGIC.C, MAGIC.D)
for i in range(0, groups, 1):
    (AA, BB, CC, DD) = (A, B, C, D)
    for j in range(0, 64, 1):
        # ABCD (initial) -> DABC (1 iter) -> CDAB (2 iter) -> BCDA (iter) -> .... 轮转起来.
        # A (initial) -> AA -> aa -> DD -> D (1 iter)
        # B (initial) -> BB -> bb -> AA -> A (1 iter) -> AA -> aa -> DD -> D (2 iter)
        (aa, bb, dd, cc) = (DD, AA, CC, BB)         # 轮转前.
        if 0 <= j <= 15:
            # 1~16 字节流, j 不动, j 分别取 0, 1, 2, 3, ..., 15.
            k = i * 64 + j * 4
            (a, b, c, d) = (AA, BB, CC, DD)
            Xk = X(decimalList[k], decimalList[k+1], decimalList[k+2], decimalList[k+3])
            a = b + AUXILIARY.L((a + AUXILIARY.F(b, c, d) + Xk + AUXILIARY.T(j+1)) & 0xffffffff, s[j])
            bb = a
            (AA, BB, CC, DD) = (aa, bb, cc, dd)     # 轮转后.
        if 16 <= j <= 31:
            # 17~32 字节流, ((5 * j) + 1) % 16, ((5 * j) + 1) % 16 分别取 1, 6, 11, 0, ..., 12.
            k = i * 64 + (((5 * j) + 1) % 16) * 4
            (a, b, c, d) = (AA, BB, CC, DD)
            Xk = X(decimalList[k], decimalList[k+1], decimalList[k+2], decimalList[k+3])
            a = b + AUXILIARY.L((a + AUXILIARY.G(b, c, d) + Xk + AUXILIARY.T(j+1)) & 0xffffffff, s[j])
            bb = a
            (AA, BB, CC, DD) = (aa, bb, cc, dd)     # 轮转后.
        if 32 <= j <= 47:
            # 33~48 字节流, ((3 * j) + 5) % 16, ((3 * j) + 5) % 16 分别取 5, 8, 11, ..., 2.
            k = i * 64 + (((3 * j) + 5) % 16) * 4
            (a, b, c, d) = (AA, BB, CC, DD)
            Xk = X(decimalList[k], decimalList[k+1], decimalList[k+2], decimalList[k+3])
            a = b + AUXILIARY.L((a + AUXILIARY.H(b, c, d) + Xk + AUXILIARY.T(j+1)) & 0xffffffff, s[j])
            bb = a
            (AA, BB, CC, DD) = (aa, bb, cc, dd)     # 轮转后.
        if 48 <= j <= 63:
            # 49~64 字节流, (7 * j) % 16, (7 * j) % 16 分别取 0, 7, 14, 5, 12, ..., 9.
            k = i * 64 + ((7 * j) % 16) * 4
            (a, b, c, d) = (AA, BB, CC, DD)
            Xk = X(decimalList[k], decimalList[k+1], decimalList[k+2], decimalList[k+3])
            a = b + AUXILIARY.L((a + AUXILIARY.I(b, c, d) + Xk + AUXILIARY.T(j+1)) & 0xffffffff, s[j])
            bb = a
            (AA, BB, CC, DD) = (aa, bb, cc, dd)     # 轮转后.
    A = A + AA
    B = B + BB
    C = C + CC
    D = D + DD

最后把迭代完成的四个幻数重新排列一下, 得到 $32\times4=128$ 比特位的 MD5 摘要结果.

幻数构成字符串按照 "ABCD" 顺序.

No description has been provided for this image
In [ ]:
# 位运算计算更快.
(A, B, C, D) = (reverse(A), reverse(B), reverse(C), reverse(D))
digest = (A << 96) | (B << 64) | (C << 32) | D
md5 = hex(digest)[2:].rjust(32, '0')
print(f'\033[33mInput: "{TRANSFORM.INPUT}" --> MD5: "{md5}"\033[0m')

Input: "Ark" --> MD5: "efa4231e24c356d525a259f0b204404e"
In [ ]:
# 字符串切片拼接更直观.
md5 = f'{hex(A)}'[2:] + f'{hex(B)}'[2:] + f'{hex(C)}'[2:] + f'{hex(D)}'[2:]
print(f'\033[33mInput: "{TRANSFORM.INPUT}" --> MD5: "{md5}"\033[0m')

Input: "Ark" --> MD5: "efa4231e24c356d525a259f0b204404e"